Solutio in silico

Compton Scattering

Compton scattering, also known as incoherent scattering, occurs when a photon interacts with an atomic electron, scattering the photon and ionizing the electron from the atom. The figure below depicts the interaction:


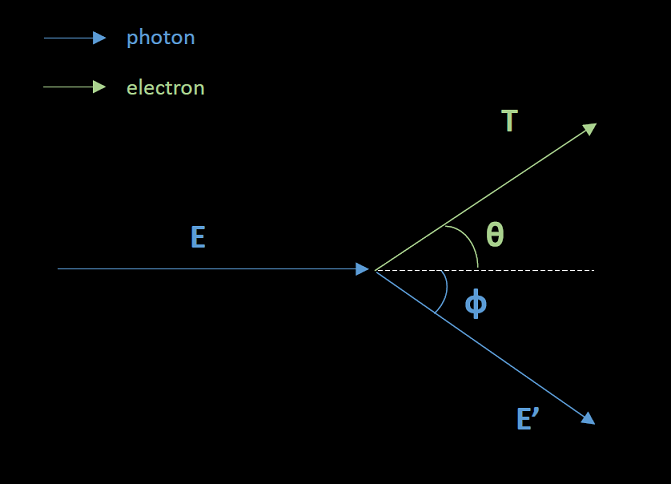
Compton Scattering

The scattered photon energy can be calculated if the scattering angle is known:

E' = \frac{E}{1 + \frac{E}{m_e c^2}(1 - cos\phi)}

The derivation of this equation is provided in one of the labs on this website.

The probability of Compton scattering can be fairly accurately calculated by assuming the electron is "free" (that is, unbound). The Compton interaction cross section for a free electron \sigma_{e^-} is calculated using the Klein-Nishina (KN) cross section equation, integrated over all scattering angles:

\sigma^{KN}_{e^-} = 2 \pi r_0 \Big\{ \frac{1+k}{k^2} \Big[ \frac{2(1+k)}{1+2k} - \frac{ln(1+2k)}{k} \Big] + \frac{ln(1+2k)}{2k} - \frac{ln(1+3k)}{(1+2k)^2} \Big\}

where the variables are repeated from the Rayleigh scattering attenuation coefficient equation. This equation, which assumes that the electron is free, agrees with experimental data for photons greater than 1 MeV; below this threshold other corrections are needed for accurate calculation. Still, from this equation we can see that the attenuation coefficient per electron is independent of atomic number and depends only on the photon energy. Calculating the KN cross section per unit mass, or the Compton mass attenuation coefficient (\sigma / \rho), simply means multiplying the KN electron cross section by the number of electrons per gram of material:

\frac{\sigma}{\rho} = \frac{N_A Z}{A} \sigma^{KN}_{e^-}

The KN notation has been dropped, but know that we are still using the KN cross section. We can see here that Compton scattering probability is dependent on N_A Z / A, the number electrons per unit mass (e.g. e- per g):

\frac{\sigma}{\rho} \propto \frac{N_A Z}{A}

\frac{\sigma}{\rho} \propto \frac{e^-}{g}

Since the ratio Z / A is relatively constant for all Z, the Compton scattering cross section is independent of atomic number. Overall, Compton scattering is the most dominant interaction for intermediate photon energies (~1-20 MeV) for low-Z materials, and therefore plays a major role in delivering dose in radiation therapy.

The mass-energy transfer coefficient for Compton scattering (\sigma_{tr} / \rho) can also be calculated using the KN cross section equation, multiplied by energy transferred per interaction and integrated over all scattering angles:

\sigma^{KN}_{e^-,tr} = 2 \pi r_0 \Big\{ \frac{2(1+k)^2}{k^2(1+2k)} - \frac{1+3k}{(1+2k)^2} - \frac{(1+k)(2k^2-2k-1)}{k^2(1+2k)^2} - \frac{4k^2}{3(1+2k)^3} - \Big[ \frac{1+k}{k^3} - \frac{1}{2k} + \frac{1}{2k^3} \Big] ln(1+2k) \Big\}

\frac{\sigma_{tr}}{\rho} = \frac{N_A Z}{A} \sigma^{KN}_{e^-,tr}

Related Links

References and Further Reading