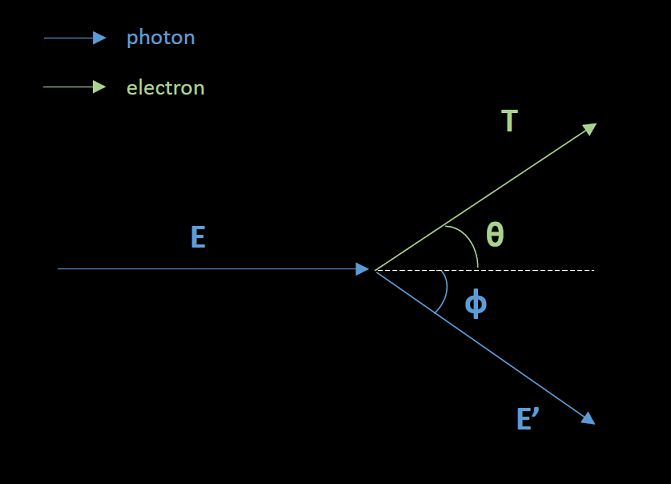
To better understand the Compton scattering equations, and to get a little math practice.
Let's start with what we know. First, for any relavitistic process both the relativisitic energy and momentum must be conserved. We will also assume at this point that the electron binding energy is negligible. Considering energy conservation (including rest mass energy) and momentum conservation, with our electron binding assumption, yields the following equations:
Energy before collision = Energy after collision
E + m_ec^2 = E' + \sqrt{p_e^2c^2 + m_e^2c^4}
Momentum before collision = Momentum after collision
\bold {p}_i = \bold {p}_f + \bold {p}_e
It is important to note that while energy is a scalar quantity, momentum is a vector; therefore both the magnitude and direction of momentum must be conserved. If we solve for the magnitude of the electron momentum |\bold{p}_e|^2 in the second equation and insert that solution into the first equation, we can derive the relationship between the initial and scattered photon energies.
First, let's square the momentum conservation equation and simplify using basic vector properties:
\bold {p}_i = \bold {p}_f + \bold {p}_e
\bold {p}_e = \bold {p}_i - \bold {p}_f
\bold {p}_e^2 = (\bold {p}_i - \bold {p}_f)^2
\bold {p}_e^2 = \bold {p}_i^2 - 2 \cdot \bold {p}_i \cdot \bold {p}_f + \bold {p}_f^2
|\bold {p}_e|^2 = |\bold {p}_i|^2 - 2 |\bold {p}_i| |\bold {p}_f| cos\phi + |\bold {p}_f|^2
p_e^2 = p_i^2 - 2p_ip_fcos\phi + p_f^2
Substitution of the photon momentum equation p=E/c produces the solution to p_e^2:
p_e^2 = \frac{E^2}{c^2} - \frac{2EE'cos\phi}{c^2} + \frac{E^{\prime 2}}{c^2}
p_e^2 = c^{-2} (E^2 - 2EE'cos\phi + E^{\prime 2})
Next, the solved value for p_e^2 will be substituted into the energy conservtion equation, which after simplification will lead to the basic Compton scatter equation. Squaring both sides of the energy conservation equation first will make the simplification easier later:
E + m_ec^2 = E' + \sqrt{p_e^2c^2 + m_e^2c^4}
(E + m_ec^2 - E')^2 = p_e^2c^2 + m_e^2c^4
(E + m_ec^2 - E')^2 = E^2 - 2EE'cos\phi + E^{\prime 2} + m_e^2c^4
E^2 + m_e^2c^4 + E^{\prime 2} + 2Em_ec^2 - 2EE' - 2E'm_ec^2 = E^2 - 2EE'cos\phi + E^{\prime 2} + m_e^2c^4
2Em_ec^2 - 2EE' - 2E'm_ec^2 = -2EE'cos\phi
Em_ec^2 - EE' - E'm_ec^2 = -EE'cos\phi
EE'cos\phi - EE' - E'm_ec^2 = -Em_ec^2
E'[E(cos\phi - 1) - m_ec^2] = -Em_ec^2
E'[m_ec^2 + E(1 - cos\phi)] = Em_ec^2
E' = \frac{Em_ec^2}{m_ec^2 + E(1 - cos\phi)}
Which, finally, simplifies to the basic Compton scattering equation:
E' = \frac{E}{1 + \frac{E}{m_e c^2}(1 - cos\phi)}